The Gyroscopic Effect
A New Explanation of an Old Phenomenon
by N. O. Williams
When the axis of a spinning body is tilted, thereby rotating its plane of spin, a so-called gyroscopic torque is developed about a third axis which is perpendicular to both the spin axis and the tilt axis. The explanation of this phenomenon as a 'first-principles' derivation always seems to be absent from applied mechanics texts, and in its place is usually given a mathematical description of the relationships between the various parameters associated with the gyroscope. There is often presented some type of mystical-sounding statement such as, "…and because the applied moment cannot change the rate of spin, it makes it rotate about a perpendicular axis instead", as if there were some kind of internal decision made by the gyroscope to opt for an alternative response.
Common sense tells us that a spinning wheel will continue to spin in the same plane unless acted upon by external forces. Unfortunately, common sense lets us down when we observe with amazement the precession of the spinning wheel as its axle is tilted. For what reason then does the spinning wheel not just simply, obligingly and passively continue to spin into a new inclined plane, without putting up a resistance in the form of a gyroscopic torque or precessing about its third axis?
What will now be presented is the 'first-principles' Newtonian mechanics explanation of how the gyroscopic torque results from the tilting of a spinning body, without having to resort to special abstract rules for the analysis of gyroscopic motion and without the help of vector mechanics.
For the purposes of this analysis, imagine we are looking down on the edge of a ring, which is merely spinning in a fixed plane, with its horizontal spin axis pointing up the page, as shown in the sketch below.
The path of each particle as it comes up towards us from θ=0°, reaches the top, and then travels back down and away from us to θ=180°, is perfectly symmetrical about the spin axis. A major illusion to be overcome in visualizing the motion of a ring, which is simultaneously spinning and tilting, is that of symmetry of motion of its constituent particles. When we view the same particle whilst the spinning ring is simultaneously tilted away from us about its horizontal tilt axis, the path of the particle mapped out in our picture plane is distinctly asymmetric. This is illustrated in the sketch below, showing the displacement locus of a particle traveling from θ=0° to θ=180° , along with the locus of its diametrically opposite number traveling from θ=180° to θ=360°.
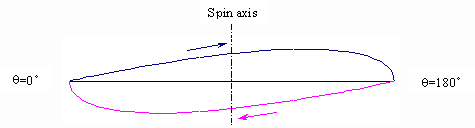
Figure 1: Plan view of the displacement loci for both diametrically opposite particles
For a ring of radius R, mass m and angular speed ω, and for a particle on that ring whose angular displacements in spin and tilt, relative to the horizontal diameter of the original spin plane, are θ and ϕ respectively, the equation of the displacement normal to the original spin plane is:
Disp.(n) = R x Sin θ x Sin ϕ
and the normal component of force on the particle as it maps out this locus is plotted in the following sketch and its magnitude is proportional to its normal component acceleration which is given by:
Acc.(n) = ω² x R x [(-Sin θ x Sin ϕ) + (2 x (ϕ / θ) x Cos θ x Cos ϕ) - ((ϕ / θ)² x Sin θ x Sin ϕ)]
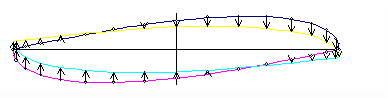
Figure 2: Distribution of the particle acceleration forces normal to the spin plane
It can be clearly seen that the sum of the normal components of acceleration forces for all particle locations in the first (θ=0° to θ=90°) quadrant is less than the sum of those in the second (θ=90° to θ=180°) quadrant. The moment arms (= R x Cos θ) of these forces in the first quadrant, relative to the centre of the ring, are equal to those in the second quadrant. Therefore, the sum of the clockwise (looking down) moments of all these component forces is greater than the sum of the anticlockwise moments about the vertical third axis (of precession) of the ring, and the sum of these moments for the whole ring is easily shown by simple manual integration to be -125% of the theoretical gyroscopic torque, m x R² x ω² x (ϕ / θ).
Similarly, the equation of the displacement of the particle in the direction parallel to the original spin plane is:
Disp.(p) = R x [1 - Cos θ] (relative to the particle initial location)
and the parallel component of force on the particle as it maps out this locus is plotted in the following sketch, and its magnitude is proportional to its parallel component acceleration which is given by:
Acc.(p) = -ω² x R x Cos θ (relative to the centre of the spin plane)
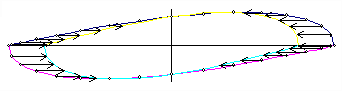
Figure 3: Distribution of the particle acceleration forces parallel to the spin plane
In this case, it can be shown that the sum of the parallel components of acceleration forces for all particle locations in the first quadrant is equal and opposite to the sum of those in the second quadrant. The moment arms (= R x (Sin θ x Sin ϕ)) of these forces in the first quadrant, relative to the centre of the ring, are less than those in the second quadrant. Consequently, the sum of the clockwise moments of all these component forces is less than the sum of the anticlockwise moments about the vertical axis of the ring, and the sum of these moments for the whole ring can be shown to be +25% of the theoretical gyroscopic torque, m x R² x ω² x (ϕ / θ).
By algebraically adding the sum of the moments of normal force components to the sum of the moments of parallel force components, we obtain a figure of -100% of the expected gyroscopic torque but, because the direction of gyroscopic reaction torque for the whole gyroscope is opposite in sign to that of the sum of moments of forces of the accelerating particles causing it, the sum of all these moments is equal to +100% of the gyroscopic torque (anticlockwise looking down).
Therefore, the asymmetric disposition of these acceleration forces and their moments about the third axis through the centre of the ring accounts exactly for the gyroscopic precession torque, both conceptually and numerically
Furthermore, the direction of the gyroscopic torque is determined directly from this analysis without resort to any arbitrary rules such as, "…the precession is such that the axis of angular momentum tends to place itself in line with the axis of the applied couple and in the same sense."
BASICS.pdf (PDF download)
Click here for Numerical Integration program listing (QuickBASIC)
Click here for Numerical
Integration check program listing, Integral.txt